 |
光伏组件
|
光伏组件
 |
光伏组件
|
光伏组件
来源:坎德拉学院
作者:Mr Kin
时间:2020-03-26
Part.1
光伏组件温度的影响因素和热模型
光伏组件运行温度受到系统设计、安装方式和气象因素等影响。设计因素包括了组件的技术类型、封装材料的类型,安装方式包括了固定支架安装(敞开式)、屋顶顺坡安装及跟踪支架安装等。气象因素包括环境温度、辐射量和风速。因此,预测户外光伏组件的运行温度是一个非常复杂的工作,需要同时考虑到上述几个因素。
在科学研究领域,建立光伏组件的热模型可以帮助量化这些因素以及估算组件的运行温度,可以降低和温度有关的不确定性,也就是说可以提高组件性能模型的准确性。经过数据量化和检验可靠的性能模型,在光伏系统设计和发电系统的仿真运行能发挥非常重要的作用。
目前关于光伏组件的热模型有多种,如基于户外实测数据的经验拟合公式或使用热传导理论进行推算。PVsyst是非常成熟的商业化光伏仿真软件,在计算组件的温度时也用到了热模型,用来表征热损耗的两个关键参数是Uc和Uv。其中Uc是一个常数,Uv是和风速有关的变量。软件内部默认三种安装方式,对应了不同的Uc和Uv经验值供用户选择。
1、Sandia组件热模型
公式如下,其中 EPOA为组件斜面辐照度,Ta为环境温度,WS为风速,a和b为常数,取决于组件的安装方式和封装材料,参考下表。
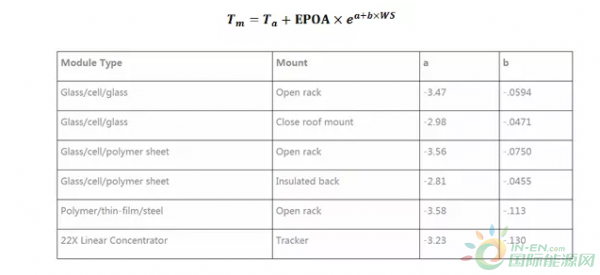
2、Faiman组件热模型
David Faiman研究团队提出了的组件热模型较为简单,根据热传导理论来确定组件温度。其中Tm为组件温度,Ta为环境温度,EPOA为光伏斜面辐照度。U0为热损失系数,为常数,U1是和风速有关的变量。WS是风速。
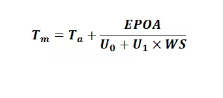
3、PVsyst组件热模型
PVsyst组件热模型是在Faiman模型的基础上发展而来,但是有点区别,温度是组件内部电池的温度。公式中Tc为电池温度,Ta为环境温度,EPOA为组件斜面辐照度,是组件实际工况下的转换效率,默认情况下是10%,α是组件电池的吸收率,默认值为0.9。U0U1为热损失系数,WS是风速。

Part.2
根据数值拟合方法确定UC和UV的流程
PVsyst软件给用户提供了三种不同安装类型的热损耗系数。如果现场有条件的话,也可以安装相应的设备进行数据采集,并通过回归分析来获得热损耗系数,这样发电量仿真的准确性就大大提高。下面提供几个步骤供参考:
1)组件户外试验平台的搭建:一般来说,光伏组件正南朝向安装,同时在组件的附近安装环境监测仪,采集组件的背板温度、风速、风向、环境温度、光伏斜面的辐照度。
2)统计时间段可采用一年或多年,后台导出辐照度、风速、组件温度、环境温度数据。
3)将数据进行过滤,减少误差,主要是筛选出上午10点至下午14点的数据。
4)计算组件背板温度与环境温度之差,即δT=Tm-Ta,计算光伏平面辐照度GlobInc与δT的比值GlobInc/δT。
5)剔除由于数据采集问题导致明显异常的计算结果。
6)绘制出GlobInc/δT与风速的拟合曲线。
7)得到曲线的截距Uc和斜率Uv。
8)根据残差分析(residual plots)做拟合性检验。做过回归分析的都知道,回归分析后的结果一定要用残差图来检查,以验证模型的可靠性。我们收集的数据,一般不可能完全服从理论的正态分布,因为理论的正态分布具有固定的概率密度函数。
那么能不能把收集的数据看作是正态的呢,这就需要通过画正态概率图来验证。正态概率图显示为直线或近似直线,就能认为残差近似服从正态分布,残差的正态概率图接近于直线,所以可以认为正态性假定成立。
Part.3
案例介绍
某户外场地安装了多块晶硅组件进行测试,样本的数据统计年份为2019年,如下图所示, 经过数据拟合以后,Uc为22.38,Uv为5.7101,拟合优度为0.6866,我们发现,该案例当风速在4米/s以上时,数据的离散性增加,因此在拟合时可采用4米/s以下的数据,将增加相关性,对于数据的拟合较为有利。
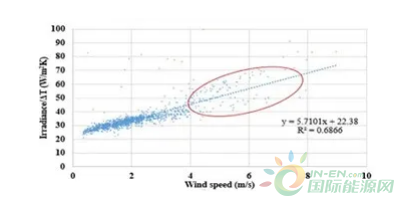
图1 数据线性拟合结果
图2为残差图和正态概率图,从图可知,残差图的形态基本上是比较满意的,正态概率图显示为直线或近似直线,残差近似服从正态分布,说明了变量风速和Irradiance/δT之间关系的回归模型是合理的,热损耗系数可以采用。

图2 残差分析和正态概率图
残差知识点
残差(Residual)是因变量的观测值y0与根据估计的回归方程求出的预测值y1之差,用e表示。它反映了用估计的回归方程去预测y0而引起的误差。第i个观察值的残差可以写为:e=y0-y1。
残差图(residual plot)是一种分析残差的有用方法,它的纵坐标(Y轴方向)是残差,横坐标(X轴方向)是x变量值或者是y变量的预测值。
为分析残差图,需要知道残差图的几种常见形态及其所反映的信息。
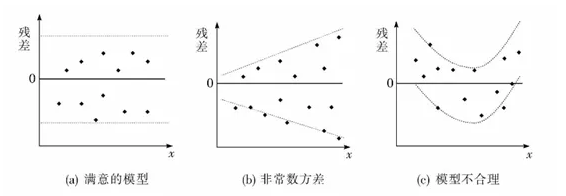
若对所有的x值,拟合值与实际值误差项ε的方差都相同,而且假定描述变量x和y之间关系的回归模型是合理的,那么残差图中的所有点都应落在一条水平带中间,如图(a)所示。但如果对所有的值,ε的方差是不同的,例如,对于较大的x值,相应的残差也较大,如图(b)所示,这就意味着违背了ε方差相等的假设。如果残差图如图(c)所示的那样,则表明所选择的回归模型不合理,这时应考虑曲线回归或多元回归模型。
国际太阳能光伏网声明:本文仅代表作者本人观点,与国际太阳能光伏网无关,文章内容仅供参考。凡注明“来源:国际太阳能光伏网”的所有作品,版权均属于国际太阳能光伏网,转载时请署名来源。
本网转载自合作媒体或其它网站的信息,登载此文出于传递更多信息之目的,并不意味着赞同其观点或证实其描述。如因作品内容、版权和其它问题请及时与本网联系。

国际能源网 28分钟前
国际能源网 34分钟前
国际能源网 43分钟前
